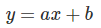Calculus and Slope

Calculus sounds really difficult. Really it is fairly simple mathematical tool. It stems from a really simple algebraic form,  the slope of a curve. All of those who have taken algebra are familiar with the slope intercept formalization of a linear curve where a is the slope coefficient and b is the y-intercept.

Calculus is concerned quite completely with the slope, or a. And indeed the derivative of this formula would be: 

The mild complexity arrives with curves that are not straight. Something like:

Source: desmos.com

Without getting bogged down in infinitesimals, it is fairly clear if you think about it that the slope of this curve is different at every point x. When a value is different for ever given value x, it too is a curve.  This curve is the derivative. In this case it is:

Source: desmos.com

You can see that where the slope is horizontal in the original curve at x = 0, the derivative is at y = 0. The derivative is just a graph of the slope of a curve. It is just a continuation of the slope intercept formalization for non-linear curves.

Some readers may have noticed that the y-intercept is not retained by the derivative. This is true. This is why when taking the integral (i.e., the opposite operation from the derivative), mathematicians always add back a constant C.  This constant is the y-intercept of the original curve. Derivatives represent only the slope and so lose this value. Using the constant makes it clear that this value was forgotten in the process of derivation.

Square Numbers

Square numbers are interesting in themselves. But there are patterns hidden in between them that can be more profound.

The difference between consecutive square numbers are the odd natural numbers. 

All square numbers are the sums of two triangle numbers. A triangle number is a number that is the sum of a consecutive list of natural numbers (i.e., 1 + 2 + 3 + 4 + 5 = 15).

This is interesting at face value alone, but this means that the sum of natural numbers up to n added to the sum of all natural numbers up to n + 1 is always a square.

And this is where you get your odd differences. To get to the next square you have to add the next natural number in each consecutive list. Since you are always adding an odd and an even, this is always the case when adding two consecutive naturals, the addend is always odd. And it can be clearly seen that the next addend is always two greater. I leave that to the reader to prove.

Another interesting fact, is that n as we have used it above is always one less then the square root of the square number sum.

Averages and Trapezoids

I rediscovered the equation for a trapezoid yesterday evening and became obsessed with it.

All night I thought of this formula and generalized it to a rectangle and a parallelogram. Nestled comfortably within the formula I found the average of two numbers.

It is easy to see that the area of a trapezoid of any kind is just the average of the lengths of its parallel edges multiplied by its height. There is a geometric significance to this fact. For a line segment running parallel to both bases through the exact middle of the shape has this magical average length. 

This can be generalized to any parallel line segments even if they are collinear. Any line segment made from the relative midpoints between the starting and ending points of these two line segments will have a length that is the average of the lengths of the other two. Perhaps one can realize the average of sets of numbers larger than two in geometry this way.